Gestión de Operaciones

Destacado

Programación Lineal (Método Gráfico)

El Método Gráfico (resolución gráfica) constituye una excelente alternativa de representación y resolución de modelos de Programación Lineal que tienen 2 variables de decisión. Para estos efectos existen herramientas computacionales que facilitan la aplicación del método gráfico como los softwares TORA, IORTutorial y Geogebra, los cuales se pueden consultar en detalle en Cómo Resolver Gráficamente un Modelo de Programación Lineal con TORA, Cómo Resolver Gráficamente un Modelo de Programación Lineal con IORTutorial y Cómo Resolver Gráficamente un modelo de Programación Lineal con Geogebra, respectivamente. En este contexto a continuación presentamos un compendio de ejercicios de Programación Lineal resueltos a través del método gráfico.

Ejercicios Resueltos del Método Gráfico en Programación Lineal

Ejercicio N°1: Una empresa vitivinícola ha adquirido recientemente un terreno de 110 hectáreas. Debido a la calidad del sol y el excelente clima de la región, se puede vender toda la producción de uvas Sauvignon Blanc y Chardonay. Se desea conocer cuánto plantar de cada variedad en las 110 hectáreas, dado los costos, beneficios netos y requerimientos de mano de obra según los datos que se muestran a continuación:

Suponga que se posee un presupuesto de US$10.000 y una disponibilidad de 1.200 días hombre durante el horizonte de planificación. Formule y resuelva gráficamente un modelo de Programación Lineal para este problema. Detalle claramente el dominio de soluciones factibles y el procedimiento utilizado para encontrar la solución óptima y valor óptimo.

Variables de Decisión:

$X_{1}$ : Hectáreas destinadas al cultivo de de Sauvignon Blanc
$X_{2}$ : Hectáreas destinadas al cultivo de Chardonay

Función Objetivo:

Maximizar $50X_{1}+120X_{2}$

Restricciones:

$X_{1}+X_{2}\leq 110$
$100X_{1}+200X_{2}\leq 10.000$
$10X_{1}+30X_{2}\leq 1.200$
$X_{1},X_{2}\geq 0$

Donde las restricciones están asociadas a la disponibilidad máxima de hectáreas para la plantación, presupuesto disponible, horas hombre en el período de planificación y no negatividad, respectivamente.

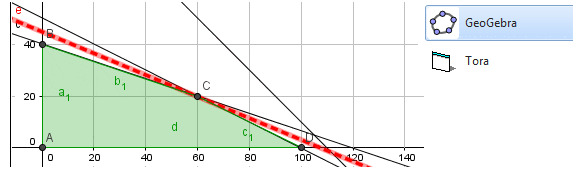
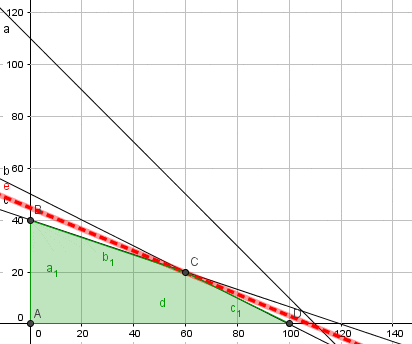
El siguiente gráfico muestra la representación del problema de la empresa vitivinícola. El área achurada corresponde al dominio de soluciones factibles, donde la solución básica factible óptima se alcanza en el vértice C, donde se encuentran activas las restricciones de presupuestos y días hombre. De esta forma resolviendo dicho sistema de ecuaciones se encuentra la coordenada de la solución óptima donde $X_{1}=60$ y $X_{2}=20$ (hectáreas). El valor óptimo es $V(P)=50(60)+120(20)=5.400$ (dólares).

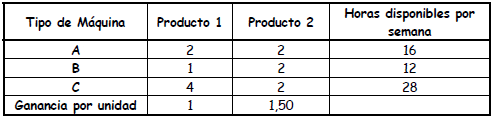
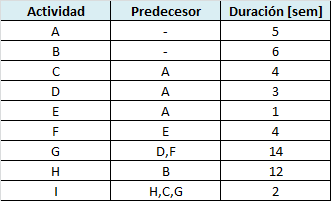
Ejercicio N°2: Un taller tiene tres (3) tipos de máquinas A, B y C; puede fabricar dos (2) productos 1 y 2, todos los productos tienen que ir a cada máquina y cada uno va en el mismo orden: Primero a la máquina A, luego a la B y luego a la C. La siguiente tabla muestra:

Las horas requeridas en cada máquina, por unidad de producto
Las horas totales disponibles para cada máquina, por semana
La ganancia por unidad vendida de cada producto

Formule y resuelva a través del método gráfico un modelo de Programación Lineal para la situación anterior que permite obtener la máxima ganancia para el taller.

Variables de Decisión:

$X_{1}$ : Unidades a producir del Producto 1 semanalmente
$X_{2}$ : Unidades a producir del Producto 2 semanalmente

Función Objetivo:

Maximizar $X_{1}+1,5X_{2}$

Restricciones:

$2X_{1}+2X_{2}\leq 16$
$X_{1}+2X_{2}\leq 12$
$4X_{1}+2X_{2}\leq 28$
$X_{1},X_{2}\geq 0$

Las restricciones representan la disponibilidad de horas semanales para las máquinas A, B y C, respectivamente, además de incorporar las condiciones de no negatividad.

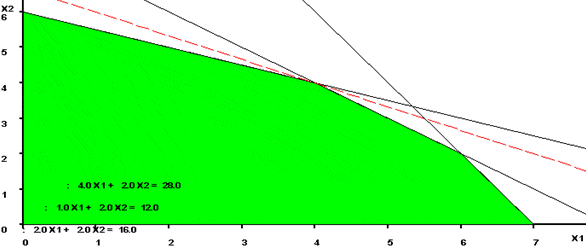
Para la resolución gráfica de este modelo utilizaremos el software GLP cual abordamos en el artículo Problema de Planificación Forestal resuelto con Graphic Linear Optimizer (GLP). El área de color verde corresponde al conjunto de soluciones factibles y la curva de nivel de la función objetivo que pasa por el vértice óptimo se muestra con una línea punteada de color rojo.

La solución óptima es $X_{1}=4$ y $X_{2}=4$ con valor óptimo $V(P)=1(4)+1,5(4)=10$ que representa la ganancia para el taller.

Ejercicio N°3: Una compañía elabora dos productos diferentes. Uno de ellos requiere por unidad 1/4 de hora en labores de armado, 1/8 de hora en labores de control de calidad y US$1,2 en materias primas. El otro producto requiere por unidad 1/3 de hora en labores de armado, 1/3 de hora en labores de control de calidad y US$0,9 en materias primas. Dada las actuales disponibilidades de personal en la compañía, existe a lo más un total de 90 horas para armado y 80 horas para control de calidad, cada día. El primer producto descrito tiene un valor de mercado (precio de venta) de US$9,0 por unidad y para el segundo este valor corresponde a US$8,0 por unidad. Adicionalmente se ha estimado que el límite máximo de ventas diarias para el primer producto descrito es de 200 unidades, no existiendo un límite máximo de ventas diarias para el segundo producto.

Formule y resuelva gráficamente un modelo de Programación Lineal que permita maximizar las utilidades de la compañía.

Variables de Decisión:

$X_{1}$ : Unidades a producir diariamente del Producto 1
$X_{2}$ : Unidades a producir diariamente del Producto 2

Función Objetivo:

Maximizar $(9-1,2)X_{1}+(8-0,9)X_{2}=7,8X_{1}+7,1X_{2}$

Restricciones:

$\frac{X_{1}}{4}+\frac{X_{2}}{3}\leq 90$
$\frac{X_{1}}{8}+\frac{X_{2}}{3}\leq 80$
$X_{1}\leq 200$
$X_{1},X_{2}\geq 0$

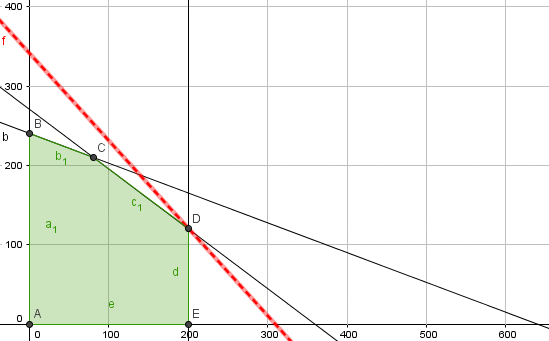
La primera restricción representa las limitantes de horas de armado diariamente. La segunda restricción la disponibilidad de horas para labores de control de calidad (también diariamente). La tercera restricción establece una cota superior para la producción y ventas diarias del Producto 1. Adicionalmente se incluyen las condiciones de no negatividad para las variables de decisión.

El dominio de soluciones factibles tiene 5 vértices que corresponden a los candidatos a óptimos del problema. En particular el vértice óptimo es D de modo que la solución óptima es $X_{1}=200$ y $X_{2}=120$ con valor óptimo $V(P)=7,8(200)+7,1(120)=2.412$ que corresponde a la utilidad máxima para la empresa.

Importante: A la fecha de esta publicación disponemos de más de 70 artículos relativos a la Programación Lineal los cuales recomendamos revisar, donde se aborda la resolución gráfica de este tipo de modelos como también la resolución a través de algoritmos como el Método Simplex y la implementación computacional con herramientas como Solver, What’sBest! y OpenSolver, entre otras.

En el siguiente tutorial de nuestro canal de Youtube se explica un ejemplo adicional con todos los elementos del método gráfico en Programación Lineal:

Destacado

Planificación de la Producción Multiproducto

El siguiente problema consiste en la formulación de un modelo de Programación Entera y posterior resolución computacional haciendo uso del complemento OpenSolver de Excel, específicamente en lo que se refiere a un modelo que permita encontrar la estrategia óptima para la Planificación de la Producción Multiproducto (es decir, 2 o más productos) y multiperiodo (2 o más períodos en el horizonte de evaluación). Referencias adicionales sobre esta clase de problemáticas pueden ser consultadas en la categoría Plan Maestro de la Producción (PMP) donde se presentan un importante volumen de ejercicios resueltos de planificación agregada. Dicho lo anterior a continuación presentamos el ejemplo objeto de nuestro análisis:

Una empresa desea optimizar la planificación de la producción de sus cinco productos principales para los primeros 6 meses del año 2016. Para el desarrollo de la tarea encomendada la empresa recolecta los siguientes antecedentes:

El proceso de fabricación es intensivo en mano de obra donde cada trabajador percibe un salario bruto de US$1.200 por una jornada de 160 horas de trabajo al mes.
El costo unitario de materiales y gastos generales, excluyendo el trabajo es de US$12 para A, US$14 para B, US$9 para C, US$13 para D y US$8 para E.
El costo de mano de obra de producción en tiempo extra se paga con un recargo de un 50% respecto a la hora trabajada en horario normal. No obstante por política de la empresa se establece un máximo de 200 horas hombre en tiempo extraordinario para cada mes, exceptuando Enero y Febrero donde el límite corresponde a 100 horas (por acuerdos con el sindicato).
El costo mensual de almacenar una unidad de cualquier producto en inventario es de US$4 por unidad. La bodega tiene una capacidad de almacenamiento de 250 unidades.
El tiempo de producción por unidad es de 5 horas para A, 6 horas para B, 8 horas para C, 4 horas para D y 3 horas para E.
La contratación de personal de producción considera un costo único de US$1.500 (adicional al sueldo) por concepto de capacitación y entrenamiento.
Para la reducción de horas de trabajo o despido considere en promedio: un sueldo de US$1.200 y una antigüedad de 2 años. Por política de estabilidad laboral se establece un máximo de despido de 6 trabajadores durante el primer semestre.
El inventario inicial corresponde a 120 y 80 unidades para los productos B y C respectivamente. No se dispone de inventario inicial para el producto A, D y E.
La planilla de trabajadores al 31 de Diciembre de 2015 es de 55 trabajadores.
Es posible dejar demanda pendiente del producto A y D asumiendo un costo unitario de US$25 en cada caso, la cual no expira y sólo se posterga para un próximo mes. No obstante la empresa requiere que como máximo queden 500 unidades de demanda pendiente (en total para la suma de ambos productos) a fines de Junio de 2016.
En cuanto al producto B, éste se puede comprar adicionalmente a un proveedor a un costo unitario de US$75. Adicionalmente el costo fijo de gestionar un pedido al proveedor del producto B (independiente del tamaño del pedido) es de US$200.
En cuanto al producto E, éste se puede comprar adicionalmente a un proveedor a un costo unitario de US$35. Adicionalmente el costo fijo de gestionar un pedido al proveedor del producto E (independiente del tamaño del pedido) es de US$150.

Formule y resuelva un modelo de optimización matemática que permita determinar la política operacional que minimice los costos totales en el horizonte de planificación y cumpla con las condiciones expuestas.

Planificación de la Producción Multiproducto

Variables de Decisión:

Notar que se dispone de 5 productos y 6 períodos. En este contexto y con el objetivo de lograr una notación más compacta se utilizan los índices i y t para representar los productos y períodos (meses), respectivamente.

Parámetros:

La definición de parámetros no es estrictamente necesaria y se realiza de modo de establecer un caso más general para el problema que facilita (compacta) la notación requerida para definir el modelo. Se puede apreciar que no todos los datos factibles de poder representar con parámetros ha sido llevado a cabo, lo cual corresponde a una decisión arbitraria la que sin embargo no afecta los resultados.

Función Objetivo:

Se busca minimizar los costos totales de la planificación multiproducto y multiperiodo. Los costos involucrados son (en orden): producción, inventario, mano de obra en tiempo normal, mano de obra en sobretiempo, contratación, despido, demanda pendiente, compra del producto B y compra del producto E.

Restricciones:

Balance de Inventario: Para el caso del producto A y D se puede utilizar demanda pendiente y para los productos B y E se pueden realizar compras. En este caso sólo los requerimientos del producto C deben ser satisfechos de forma exclusiva a través de la producción e inventario.

Balance de Trabajadores: La cantidad de trabajadores disponibles en un mes para funciones de producción será igual a los disponibles en el mes anterior, más los contratados en el mes y menos los despedidos en dicho mes.

Capacidad de Producción: El lado izquierdo de la restricción representa la cantidad de horas requeridas en un mes para la producción de los 5 productos, lo cual no podrá superar las horas disponibles (siendo éstas las horas en tiempo normal más las horas que eventualmente se utilicen en sobretiempo).

Capacidad de la Bodega: Para cada mes del horizonte de planificación la cantidad de productos almacenados en inventario (suma de todos los productos) no podrá superar la capacidad de almacenamiento de la bodega de 250 unidades.

Máximo de Compras B y E: La cantidad máxima de compra para el producto B y E dependerá si se adopta la decisión de realizar una compra en el mes respectivo. En dicho caso la cantidad máxima a comprar corresponderá a los parámetros o constantes grandes $M_{B}$ y $M_{E}$ , respectivamente. Por ejemplo un valor para $M_{B}$ podría ser 3.152 que corresponde a la suma de la demanda del producto B del mes 1 al mes 6.

Máxima Cantidad de Despidos: Durante el horizonte de planificación no se pueden despedir más de 6 trabajadores.

Máximo Demanda Pendiente Mes 6: Al final del mes 6 no debe quedar más de 500 unidades de demanda pendiente para el producto A y D (en conjunto).

No Negatividad y Enteros: Las variables de decisión deben adoptar no negativos y enteros (exceptuando las variables binarias).

La implementación computacional con OpenSolver del modelo de optimización anterior entrega los siguientes resultados. Las celdas en color amarillo corresponden a las variables de decisión del problema definidas inicialmente que satisfacen las restricciones impuestas (solución factible).

El valor óptimo corresponde a US$599.770 que corresponde al costo mínimo asociado al plan de producción. A continuación se desglosa dicho costo total en los distintos ítems de costos según lo detallado anteriormente.

¿Quieres tener la planilla Excel con la resolución en OpenSolver de este problema?.

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]

Destacado

Cómo obtener la Ruta Crítica de un Proyecto (Critical Path Method)

El método de la Ruta Crítica conocida también por CPM por sus siglas en inglés (Critical Path Method) es una metodología de la Gestión de Proyectos que nos permite entre otros aspectos estimar la duración de un Proyecto. Para este propósito es necesario conocer las actividades que contempla el proyecto, su duración en una unidad de tiempo y el orden en el cuál deben ser realizadas (por ejemplo, algunas actividades se pueden desarrollar sólo cuando una o varias actividades previas o predecesoras han sido completadas).

Cómo obtener la Ruta Crítica de un Proyecto

El ejemplo a continuación muestra en detalle la aplicación del Método de Ruta Crítica a un proyecto que consta de 9 actividades cuyos tiempos estimados se encuentran en semanas. Adicionalmente en la columna «Predecesor» se establece el orden en el cual se deben realizar las distintas actividades, por ejemplo, la Actividad G se puede realizar una vez completada las Actividades D y F.

En este contexto resulta de utilidad desarrollar un Diagrama o Representación Gráfica del Proyecto donde cada nodo representa una actividad, el número al interior del paréntesis la duración de dicha actividad, y las flechas un camino o ruta consistente con las relaciones de precedencia.

Por ejemplo, la Actividad G tiene una duración estimada de 14 semanas y dicha actividad se puede iniciar una vez que hayan concluido sus predecesores, es decir, las Actividades D y F.

Se puede observar adicionalmente que las actividades iniciales son A y B y la actividad final es I.

Una actividad inicial es aquella que se puede comenzar inmediatamente y no existe ninguna otra actividad que le precede.
Una actividad final es una actividad que termina una ruta o camino del proyecto y en consecuencia no es predecesora de ninguna otra actividad del proyecto.

Por tanto la duración del proyecto estará determinado por aquella ruta o camino más largo que comenzando en una actividad inicial concluya en una actividad final. En nuestro ejemplo, un camino que comenzando en A (o en B) termine en I.

Luego, dado el tamaño reducido de este ejemplo es posible enumerar todas las posibilidades rutas o caminos que satisfacen la condición anterior:

Ruta: A-C-I: 5[sem]+4[sem]+2[sem]=11[sem]
Ruta: A-D-G-I: 5[sem]+3[sem]+14[sem]+2[sem]=24[sem]
Ruta: A-E-F-G-I: 5[sem]+1[sem]+4[sem]+14[sem]+2[sem]=26[sem]
Ruta: B-H-I: 6[sem]+12[sem]+2[sem]=20[sem]

La Ruta Crítica por tanto es A-E-F-G-I lo que determina que la duración del proyecto es de 26[sem].

Adicionalmente podemos estimar cuándo es lo más pronto que se puede comenzar cada actividad (inicio más cercano o IC – color rojo) y cuándo es lo más pronto que se puede terminar una actividad (término más cercano o TC – color azul).

Por ejemplo, para obtener el inicio más cercano y el término más cercano, en el caso de la Actividad A, éste será la semana 0 y 5, respectivamente. De la misma forma, lo más pronto que puede comenzar la Actividad C será en la semana 5 (tan pronto concluyo su predecesor que es la Actividad A) y lo más pronto que puede terminar es en la semana 9 (dado que la duración de la Actividad C es de 4 semanas) y así se continua el procedimiento desde el inicio hasta el final del proyecto.

En forma complementaria se puede obtener el tiempo más lejano en el cual se puede terminar una actividad sin atrasar el proyecto (término más lejano o TL – verde) y cuándo es lo más tarde que se puede comenzar una actividad sin retrasar el proyecto (inicio más lejano o IL – naranjo). Para obtener dichos tiempos retrocedemos desde la actividad final (I) hacia las actividades iniciales (A y B).

Por ejemplo, lo más tarde que puede terminar la Actividad H sin retrasar el proyecto es en la semana 24 (si termina más tarde de ello, entonces la Actividad I no se podrá iniciar en la semana 24 y por tanto el proyecto terminará más tarde que la semana 26). Naturalmente dado lo anterior, la Actividad H no podrá comenzar más tarde que la semana 12 si es que se desea terminar el proyecto en 26 semanas.

En este contexto se define el término Holgura (H) o Slack como el tiempo máximo que una actividad se puede retrasar en su inicio sin que esto afecte el tiempo estimado para terminar el proyecto como un todo:

Holgura = IL – IC = TL – TC

El siguiente diagrama muestra la ruta del proyecto con el cálculo de las holguras de cada una de las actividades. Se puede apreciar por ejemplo que la actividad B se puede retrasar un máximo de 6[sem] (su holgura) y aun así estar en condiciones de terminar el proyecto en 26[sem].

Adicionalmente las actividades que pertenecen a la ruta crítica tienen holgura igual a cero, lo que en este ejemplo en particular permite identificar una ruta única: A-E-F-G-I (notar que en general un proyecto puede tener más de una ruta o camino crítico).

Actualización: De forma de corroborar los resultados anteriores, a continuación se presenta una Carta Gantt del Proyecto obtenido a través del Método de Ruta Crítica (CPM). Con color rojo se destacan aquellas actividades que forman parte de la ruta crítica con holgura igual a cero.

Análisis ABC de Ventas de Productos mediante un Diagrama de Pareto

Uno de los aspectos claves en la competitividad de una Cadena de Suministro es tomar decisiones acertadas en cuanto a los tamaños de pedidos a realizar a los proveedores, teniendo en consideración un entorno con una demanda incierta o aleatoria (es decir, que no se tiene certeza del valor que adquirirá dicha variable de antemano) y productos con distinto ciclo de vida. En este contexto las metodologías cuantitativas constituyen una contribución en este desafío de determinación de pedidos óptimos, siendo el Análisis ABC de la venta de los productos una de sus principales herramientas.

Análisis ABC de Ventas

Consideremos una empresa que maneja sólo 14 SKU (Stock Keeping Unit) y que ha recolectado la estadística de ventas de cada uno de sus productos en el último año (por ejemplo se vendieron 207 unidades del producto A en el mes de Enero). Los datos se resumen a continuación:

La Venta Promedio (PROM) del producto A es de 334,8 unidades (se obtiene simplemente de la sumatoria de las ventas de Enero a Diciembre de dicho producto dividido en 12 meses, es decir, (207+293+200+…+412)/12=334,8). La Desviación Estándar (D.EST) de la venta del producto A es de 116,9 unidades y el Coeficiente de Variación (CV) o Índice de Variabilidad se obtiene al dividir la Desviación Estándar por la Venta Promedio. Por cierto los cálculos se facilitan al hacer uso de una planilla Excel, lo cual ahorra esfuerzos en la medida que se trabaja con un número creciente de productos.

A continuación se desarrolla un Análisis ABC de la venta de los productos el cual se basa en la aplicación de la Regla de Pareto. Para ello se ordena en forma descendente los productos según los datos de la columna Venta Promedio (PROM) en color amarillo, luego se calcula cuánto representa dicho promedio respecto a la sumatoria de todos los promedios (que es 2.866,4 unidades), por ejemplo, para la SKU E es 1.666,7/2.866,4=58,14% (aprox). Finalmente la última columna (% ACU.) corresponde al porcentaje acumulado de la venta total de productos para un cierto nivel de SKU acumuladas (por ejemplo, en conjunto los productos E, A y B corresponden al 80,40% de la venta total).

El Diagrama de Pareto correspondiente a los datos anteriores se puede obtener fácilmente haciendo uso de Excel según detallamos en el artículo Cómo hacer un Diagrama de Pareto con Excel 2010.

La información obtenida a través del análisis ABC de venta de productos es útil toda vez que orienta respecto a aquellos productos con mayor rotación de inventarios, la variabilidad de la demanda y la concentración de la venta en distintos SKU. Todos estos elementos orientan la toma de decisiones y permite priorizar de mejor forma las distintas iniciativas en la Gestión de la Cadena de Suministro (SCM), buscando garantizar el suministro en tiempo y cantidad de aquellos productos que son los más relevantes para la empresa.

Suavizamiento Exponencial Simple (Ejercicios Resueltos)

El método de Suavizamiento Exponencial Simple (conocido también como Alisamiento Exponencial o Suavización Exponencial Simple) corresponde a una de las metodologías más populares para realizar Pronósticos de Demanda al disponer de una serie de tiempo. En este contexto en el artículo Pronóstico de Demanda con Alisamiento Exponencial para distintos valores de Alfa se detalla la aplicación de este método simulando su comportamiento y ajuste a los datos de la demanda real para distintos valores del parámetro de suavización alfa (α). A continuación presentaremos un compendio de ejercicios resueltos de Suavizamiento Exponencial Simple y un resumen de los principales conceptos tras este método.

El pronóstico del período t ( $F_{t}$ ) será igual al pronóstico del período anterior, es decir, del período t-1 ( $F_{t-1}$ ) más alfa (α) por el error del período anterior ( $A_{t-1}-F_{t-1}$ ), según se muestra en la fórmula a continuación:

Ejercicios Resueltos de Suavizamiento Exponencial Simple

Ejercicio N°1: Una empresa de consumo masivo lleva registro de la demanda mensual de uno de sus productos emblemáticos para un período de un año. Dicha información se presenta en la columna etiquetada Demanda en la imagen a continuación. Se requiere utilizar el método de suavizamiento exponencial simple considerando tres valores para el parámetro de suavizamiento alfa: 0,1; 0,5 y 0,9. Obtener el pronóstico del período 13 (mes de Enero del año siguiente) y evaluar el ajuste del método para cada uno de los valores de alfa propuestos.

Recordar que el suavizado exponencial simple requiere de un primer pronóstico para su aplicación. En este caso hemos decidido generar un pronóstico a contar del segundo período (mes de Febrero) y asumir que dicho valor corresponde a la demanda real del mes anterior (mes de Enero o período 1). Este criterio por cierto es arbitrario y se podría seleccionar otro punto de partida, por ejemplo, un promedio para la demanda real de los 12 meses.

Adicionalmente en las columnas E, F y G de la imagen anterior se observa los pronósticos para alfa 0,1, 0,5 y 0,9, respectivamente. En particular se puede corroborar la fórmula utilizada para obtener el pronóstico del mes de Febrero utilizando α=0,1 (celda E5), donde los resultados han sido aproximados al entero más cercano.

Ejercicio N°2: Considerando la información del Ejercicio N°1 ¿Cuál de los 3 métodos tiene asociado una menor Desviación Absoluta Media (MAD)?.

Para obtener el MAD (Mean Absolute Deviation) o Desviación Absoluta Media, aplicamos el procedimiento descrito en el artículo Calculo del MAD y la Señal de Rastreo para un Pronóstico de Demanda. En la planilla interactiva a continuación puedes simular tanto los pronósticos como el comportamiento del MAD para distintos valores de alfa. Para ello basta con editar las celdas en color amarillo.

En caso de obtener un error del tipo #VALUE! ingrese los valores de α utilizando . (punto) como separador de decimal, por ejemplo, α=0.1.

Conclusión: El alfa que provee el menor MAD al período 12 entre las 3 alternativas evaluadas (0,1, 0,5 y 0,9) es α=0,1 (MAD de 449,7). En efecto se puede corroborar utilizando el módulo Predictor de Crystal Ball (según se describe en Cómo utilizar el Módulo Predictor en Crystal Ball para Promedio Móvil Simple y Suavizado Exponencial Simple) que α=0,001 es el valor de alfa que minimiza el MAD en este ejemplo.

Ejercicio N°3: Asuma nuevamente la información del Ejercicio N°1 ¿Cuál de los 3 métodos tiene asociado un menor Error Porcentual Absoluto Medio (MAPE)?.

A continuación se presentan los resultados del cálculo del MAPE donde en particular se puede observar que la fórmula de cálculo es simplemente el promedio de los errores absolutos en términos porcentuales. Luego se concluye que al igual que en el Ejercicio N°2 el parámetro alfa que tiene mejor desempeño en relación al MAPE es α=0,1.

Observación: En la pantalla de los resultados obtenidos con Predictor de Crystal Ball se observa que para α=0,001 el valor del MAPE es 22,43%. Te recomendamos verificar el resultado anterior haciendo uso del procedimiento anteriormente descrito.

Ejercicio N°4: Calcule y grafique la Señal de Rastreo (Tracking Signal o TS) para los métodos aplicados en el Ejercicio N°1.

Se observa que la Señal de Rastreo se encuentra en los límites comúnmente aceptados [-4,4] MAD. Adicionalmente no se observa una tendencia evidente en su comportamiento por lo cual no se evidencia la presencia de error sistemático. Criterios y antecedentes similares sobre la interpretación conceptual de este indicador de desempeño se aborda en el artículo Interpretación de la Señal de Rastreo de un Pronóstico de Demanda.

Conclusión: En general el método de Suavizamiento de Exponencial Simple tiene un mejor desempeño cuando la serie de tiempo no presenta tendencia ni estacionalidad marcada. En el caso de evidenciar alguno de estos componentes en la serie de tiempo (o ambos de forma simultanea) se recomienda explorar otros métodos de pronóstico como el Método de Suavizamiento Exponencial Ajustado a la Tendencia (Suavización Exponencial Doble) o el Método de Descomposición (entre otros).

Qué es el Diagrama de Ishikawa o Diagrama de Causa Efecto

El Diagrama de Ishikawa o Diagrama de Causa Efecto (conocido también como Diagrama de Espina de Pescado dada su estructura) consiste en una representación gráfica que permite visualizar las causas que explican un determinado problema, lo cual la convierte en una herramienta de la Gestión de la Calidad ampliamente utilizada dado que orienta la toma de decisiones al abordar las bases que determinan un desempeño deficiente.

La utilización del Diagrama de Ishikawa se complementa de buena forma con el Diagrama de Pareto el cual permite priorizar las medidas de acción relevantes en aquellas causas que representan un mayor porcentaje de problemas y que usualmente en términos nominales son reducidas.

La estructura del Diagrama de Ishikawa es intuitiva: identifica un problema o efecto y luego enumera un conjunto de causas que potencialmente explican dicho comportamiento. Adicionalmente cada causa se puede desagregar con grado mayor de detalle en subcausas. Esto último resulta útil al momento de tomar acciones correctivas dado que se deberá actuar con precisión sobre el fenómeno que explica el comportamiento no deseado.

En este contexto, una representación del Diagrama de Causa Efecto o Diagrama de Espina de Pescado tiene la siguiente forma:

Con el propósito de ser más específico consideremos que se desea analizar las razones que determinan que un auto (vehículo) no encienda. Los motivos pueden ser variados:

Problemas en el Motor (correa de transmisión dañada, motor de partida dañado, etc).
Insumos o materiales (batería descargada, sin combustible, etc)
Métodos utilizados (engranaje en posición incorrecta, etc)
Problemas asociados al personal (falta de mantenimiento, falta de entrenamiento, etc)
Condiciones ambientales (clima frío)

Como se puede observar cada causa puede tener subcausas, por ejemplo, es posible que el auto no encienda por un problema en el motor, en específico porque éste está sobrecalentado. Así también es posible que el auto no encienda por problemas de materiales, por ejemplo, la batería no tiene carga (notar que sería posible seguir detallando subcausas adicionales dado que el hecho que una batería este descargada se puede deber al cumplimiento de su vida útil o a que el usuario se olvido de apagar las luces del auto al llegar a su casa).

Una versión ampliada de la imagen anterior se puede descargar de https://www.gestiondeoperaciones.net/wp-content/uploads/2014/12/diagrama-de-ishikawa-2.gif. El Diagrama de Ishikawa fue realizado utilizando el Software SmartDraw el cual dispone de una versión de evaluación que puede ser descargada desde su página web.

Una vez confeccionado el Diagrama de Ishikawa se sugiere evaluar si se han identificado todas las causas (en particular si son relevantes), y someterlo a consideración de todos los posibles cambios y mejoras que fueran necesarias. Adicionalmente se propone seleccionar las causas más probables y valorar el grado de incidencia global que tienen sobre el efecto, lo que permitirá sacar conclusiones finales y aportar las soluciones más aconsejables para resolver y controlar el efecto estudiado.

Finalmente y a modo de consolidar los conceptos anteriormente presentados, a continuación se observa un Diagrama de Espina de Pescado que aborda el problema de entrega tardía que podría enfrentar un local de venta de pizzas los fines de semana (esto corresponde al efecto). Al igual que en el ejemplo del vehículo, se identifican potenciales causas y en un nivel de detalle mayor subcausas que podrían explicar el efecto no deseado en el atraso de entrega de las pizzas.

Cómo hacer un Diagrama de Pareto con Excel 2010

El Diagrama de Pareto consiste en una representación gráfica de los datos obtenidos de un problema que resulta de utilidad para identificar cuáles son los aspectos prioritarios que se deben enfrentar. En este contexto se espera el cumplimiento de la Regla de Pareto que empíricamente indica que aproximadamente el 80% de los problemas se explica por aproximadamente el 20% de las causas (notar que la Regla de Pareto se aplica adicionalmente en otros ámbitos y que por cierto los porcentajes anteriores son aproximaciones).

En el siguiente artículo desarrollamos a través de un ejemplo la confección de un Diagrama de Pareto haciendo uso de Excel en su versión de Office 2010, no obstante, resulta ser bastante genérico como instructivo en caso que estemos utilizando otra versión de Office.

Para ello consideremos la observación de un proceso de manufactura de computadores donde se lleva registro de todas las causas (se han identificado 10) que generan un rechazo en el control de calidad durante el horizonte de evaluación.

Por ejemplo la Causa 1 ha representado un total de 182 defectos (de un total de 355 defectos detectados) lo que corresponde a un 51,27% del total (182/355=0,5127). Notar que en conjunto la Causa 1 y Causa 2 representan un 80,28% del total (285/355=0,8028) lo cual aproxima de forma cercana el cumplimiento de la regla empírica de Pareto. A continuación una descripción detallada del procedimiento en Excel para la confección del Diagrama de Pareto.

Paso 1: Seleccionamos los datos de las columnas «Causas», «N° Defectos» y «% Total Acum.». A continuación en el Menú «Insertar» seleccionamos gráfico de «Columna», luego en las opciones disponibles en «Columna en 2-D» la alternativa «Columna agrupada».

Paso 2: Al completar el Paso 1 se generará un diagrama de barra como el que se muestra en la imagen a continuación. Luego debemos seleccionar cuidadosamente el eje horizontal (que representan el % Total Acum.) y posteriormente procedemos a «Cambiar tipo de gráfico».

Paso 3: Se desplegará una ventana que permite cambiar el tipo de gráfico donde debemos seleccionar «Línea» y «Aceptar».

Paso 4: Una vez concluido el Pase 3 obtendremos un gráfico como el que se muestra en la siguiente imagen. Seleccionamos con doble clic cualquiera de los datos que representa la serie de línea «% Total Acum.» (en el ejemplo el dato correspondiente a la Causa 9).

Paso 5: En la ventana «Formato de serie de datos» en «Opciones de serie» seleccionamos «Eje secundario» y luego «Cerrar». Se debería obtener un gráfico como el que se muestra a continuación.

Paso 6: Nuestro Diagrama de Pareto ha sido confeccionado y debería ser de la siguiente forma:

Opcionalmente se pueden hacer algunos cambios adicionales como, por ejemplo, dejar la etiqueta de datos al pie del gráfico y ajustar la escala del eje vertical de porcentajes de modo que el máximo valor sea un 100%.

Una vez concluida la construcción del Diagrama de Pareto la interpretación de los datos se facilita, donde se observa tanto la frecuencia absoluta asociada a cada causa (que gatilla en un defecto) como también la contribución relativa acumulada que generan determinadas causas en el total de los defectos.

Notar adicionalmente que es imprescindible realizar un diagrama de causas (por ejemplo, el Diagrama de Espina de Pescado o Diagrama de Ishikawa) si se quieren realizar mejoras. De esta forma se puede intervenir el Proceso Productivo en aquellos aspectos que están causando un desempeño deficiente y que se ve traducido en la calidad desmejorada del producto.

A continuación el enlace de descarga del archivo Excel utilizado en este artículo: Excel Diagrama de Pareto y un vídeo de nuestro canal de Youtube con el detalle de la implementación computacional:

Adicionalmente dejamos a disposición de nuestros usuarios la siguiente plantilla Excel la cual puede ser editada y ver los cambios asociados en la forma del Diagrama de Pareto:

¿Quieres tener el archivo Excel con el Diagrama de Pareto de este Ejemplo?

[sociallocker]

MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO

[/sociallocker]