Según hemos abordado en artículos anteriores el Precio Sombra de una restricción representa la tasa de cambio del valor óptimo ante una modificación marginal del lado derecho de una restricción. Se entiende por «marginal» aquella modificación que no cambia la geometría del problema, es decir, que la nueva solución óptima se puede encontrar a través de la resolución del sistema de ecuaciones al que da origen las restricciones activas originales (previa actualización del parámetro que estamos modificando). En este contexto el precio sombra puede ser un valor positivo, negativo o cero y en particular nos referiremos a este último caso en este artículo.
Consideremos el siguiente modelo de Programación Lineal en 2 variables:
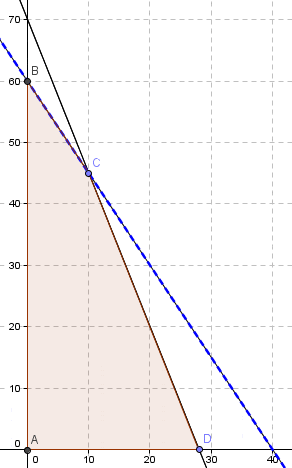
El problema anterior lo podemos resolver gráficamente utilizando Geogebra, que da origen a un problema con infinitas soluciones óptimas en el tramo de recta que une los vértices B y C y que se puede denotar de forma general por: (X,Y)=λ(0,60)+(1-λ)(10,45) con λ en el intervalo entre [0,1]. El valor óptimo en consecuencia es V(P)=1.200.
¿Cuáles son las restricciones activas en el óptimo?. Por ejemplo si consideramos el vértice B (solución óptima) las restricciones activas son 3X+2Y<=120 y X>=0, sin embargo si seleccionamos el vértice C (también solución óptima) las restricciones activas son 5X+2Y<=140 y 3X+2Y<=120. Dado lo anterior ¿aumentará el valor óptimo si se dispone de unidades adicionales del recurso que representa el lado derecho de la restricción 5X+2Y<=140?.
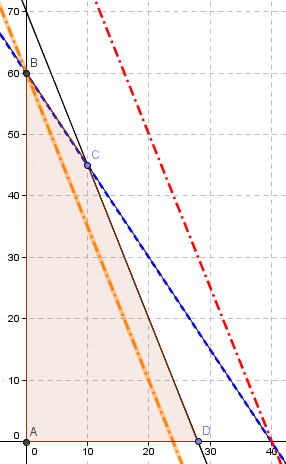
Para ello buscaremos mantener activas las restricciones del vértice C identificando la máxima variación (aumentando el valor del lado derecho) que conserve las restricciones activas originales (esto genera un desplazamiento paralelo de la restricciones que hemos representado con la línea color punteada color rojo) lo cual se alcanza en la coordenada (X,Y)=(40,0). De forma análoga para determinar la mínima variación para el lado derecho desplazamos en un sentido de decrecimiento la restricción buscando conservar las restricciones activas originales hasta la coordenada (X,Y)=(0,60) (línea punteada color naranjo).
Evaluamos en la fórmula para el cálculo del precio sombra obteniendo lo siguiente:
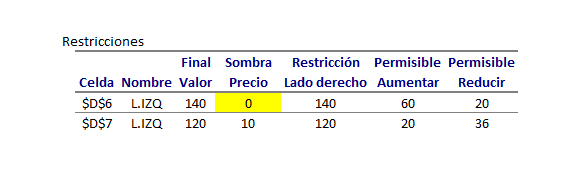
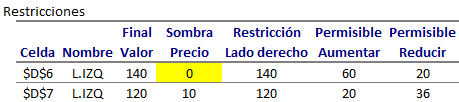
Por tanto el precio sombra de la restricción 1 (5X+2Y<=140) es cero lo cual indica que si aumenta o disminuye el valor del parámetro que representa su lado derecho (actualmente b1=140) en el intervalo entre [120,200] no se verá afectado el valor óptimo del problema. Lo anterior es consistente con lo obtenido a través del informe de confidencialidad de restricciones de Solver de Excel:
En general un precio sombra igual a cero significa que la modificación del parámetro que representa el lado derecho de la respectiva restricción (en un intervalo que conserva la geometría del problema) no tiene un impacto en el valor óptimo del problema. Sin embargo, existen casos especiales como los problemas de Programación Lineal que admiten infinitas soluciones (como el descrito en este artículo) donde una restricción con precio sombra igual a cero puede ser activa en uno de los vértices óptimo (el caso más usual es que una restricción con precio sombra igual a cero no sea activa en el óptimo).
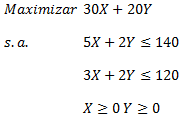
muy bueno, me aclaró ciertas dudas que tenia…….gracias
Estimados,
Para el caso de soluciones infinitas, debo hacer el análisis para ambos puntos extremos del trazo de puntos, es decir en el ejemplo analizo para C fijo y luego repito el análisis para B fijo, y reporto ambas como respuesta a un análisis de sensibilidad de precio sombra para la restricción 1???
Gracias de antemano,
atte.,
Carolina
@Carolina. No es necesario hacer el análisis por separado para cada punto extremo. Puedes notar, por ejemplo, que la restricción activa esta activa sólo en el vértice (óptimo) C pero que en todas las soluciones que representa el tramo BC (excluyendo C por supuesto) la restricción 1 no es activa. Luego, el precio sombra de la restricción 1 es cero. Lo anterior se puede corroborar a través del Método Simplex: en el tableau óptimo el costo reducido de la variable de holgura de la restricción 1 será 0.