Una de las aplicaciones clásicas de la Programación Lineal es el Problema de la Dieta. El objetivo es seleccionar un conjunto de alimentos dados que permitan satisfacer ciertos requerimientos nutricionales y preferencias y que adicionalmente tenga un costo mínimo.
En este contexto en el Servidor NEOS se puede encontrar un conjunto de antecedentes que permiten comprender el contexto histórico del Problema de la Dieta y cómo se puede abordar de forma eficiente a través de modelos de optimización. Al igual que varias de las aplicaciones de la Investigación de Operaciones este problema tiene un origen militar.
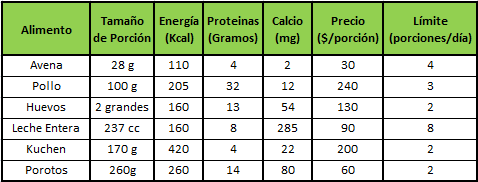
Para efectos de este tutorial y con el objetivo de ilustrar esta aplicación consideremos el siguiente listado de alimentos con su perfil nutricional y costo monetario:
Se desea proponer una dieta que contenga al menos 2.000 (Kcal) , al menos 55 gramos de proteína y 800 (mg) de calcio. Adicionalmente para garantizar cierta variedad en la dieta se establece límites de porciones por día en los alimentos. Con esta información se requiere encontrar la dieta que tenga el menor costo asociado y permita satisfacer los requerimientos anteriores.
Para ello definimos el siguiente modelo de Programación Lineal:
1. Variables de Decisión: Xi : Porciones de alimentos a consumir durante el día del alimento i (Con i=1 ==> Avena, …. i=6 ==> Porotos).
2. Función Objetivo: Minimizar 30X1+240X2+130X3+90X4+200X5+60X6
3. Restricciones:
- Mínimo de Calorias (KCal): 110X1+205X2+160X3+160X4+420X5+260X6 >= 2.000
- Mínimo de Proteínas: 4X1+32X2+13X3+8X4+4X5+14X6 >= 55
- Mínimo de Calcio: 2X1+12X2+54X3+285X4+22X5+80X6 >= 800
- Variedad de la Dieta: X1<=4 X2<=3 X3<=2 X4<=8 X5<=2 X6<=2
- No Negatividad: Xi>=0 Para todo i.
La implementación de este modelo en Solver de Excel para obtener su solución óptima y valor óptimo se muestra en el siguiente tutorial:
La Solución Óptima es X1=4, X2=0, X3=0, X4=2,08, X5=1,68, X6=2 y el Valor Óptimo (costo de la dieta) es $764,07.
Como el modelo es de Programación Lineal se permiten valores fraccionarios para las variables de decisión. Por tanto si buscamos solo valores enteros para las variables de decisión en ese caso debemos definir un modelo de Programación Entera el cual revisamos en el siguiente artículo: Problema de la Dieta en Programación Entera resuelto con Solver de Excel.

Bueno. Tengo una observación: quiero profundizar en SOLVER con sus OPCIONES y con los resultados…. es decir, que le dicen al investigador con un lenguaje claro, conciso y directo. GRACIAS Y ÉXITOS desde COLOMBIA.
Estamos aquí para ayudarte. Saludos!
como se resuelve manualmente
@jorge. Si bien se puede resolver manualmente (por ejemplo utilizando el Método Simplex de 2 Fases) no tiene mayor utilidad práctica intentarlo dado el tamaño del problema.
Estimado, muchas gracias por la explicación, la verdad que tengo unas dudas, ya que estoy tratando de resolver un ejercicios muy similar, sin embargo tengo unas dudas con los valores resultados (sobre todo cuando la variable me da 0) es posible que me puedas ayudar?
Desde ya muchas gracias.
@Juan Carlos: Puedes enviar tu ejercicio a info@gestiondeoperaciones.net para que podamos evaluar su resolución. Saludos.
Excelente Tutorial
Hola Geo, tengo que presentar un proyecto utilizando esa herramienta pero no se como usar solver. ¿Es un software que debo comprar? son cuatro cuadritos que debo realizar, donde debo minimizar costos y minimizar calorías, es sencillo. Además mi pregunta es ¿puedo eso hacerlo a mano?
@Carmen: No es difícil activar el complemento Solver en Excel. Puedes seguir los pasos detallados en http://www.investigaciondeoperaciones.net/instalacion_solver_excel.html . Envíanos tu problema escribiendo a info@gestiondeoperaciones.net para sugerirte cómo se puede resolver.