Cómo se relaciona el Coeficiente de Correlación de Pearson (r) y el Coeficiente de Determinación r Cuadrado (r²)

El coeficiente de correlación de Pearson o r es una prueba estadística que permite analizar la relación entre dos variables medidas en un nivel por intervalos o de razón, donde r mide el grado de asociación lineal entre dos variables X e Y. La prueba en sí no considera a una como independiente y a otra como dependiente, ya que no se trata de una prueba que evalúa causalidad. El coeficiente r de Pearson se estima de acuerdo a la siguiente fórmula:

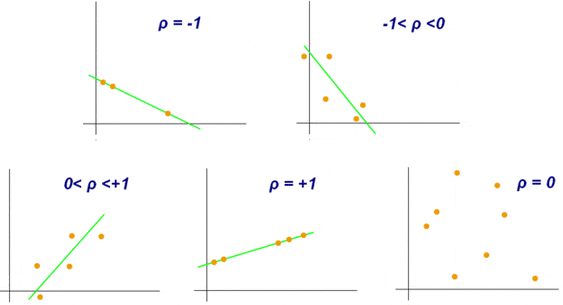
El coeficiente r de puede variar de -1 a 1, donde el signo indica la dirección de la correlación y el valor numérico, la magnitud de la correlación. En este contexto se resumen algunos criterios de interpretación:

• -1,00 = Correlación negativa perfecta
• -0,90 = Correlación negativa muy fuerte
• -0,75 = Correlación negativa considerable
• -0,50 = Correlación negativa media
• -0,10 = Correlación negativa débil
• 0,00  = No existe correlación lineal alguna entre las variables
• 0,10  = Correlación positiva débil
• 0,50  = Correlación positiva media
•  0,75 = Correlación positiva considerable
•  0,90  = Correlación positiva muy fuerte
• 1,00  = Correlación positiva perfecta

A continuación se presentan algunos ejemplos de diagramas de dispersión con diferentes valores del coeficiente de correlación de Pearson (poblacional).

Cuando el coeficiente r de Pearson se eleva al cuadrado, el resultado indica el porcentaje de la variación de una variable debido a la variación de la otra y viceversa. Es decir, el coeficiente de determinación, r al cuadrado o r², es la proporción de la variación en Y explicada por X. Puede adoptar cualquier valor entre 0 y 1, inclusive.

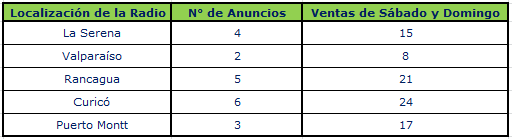
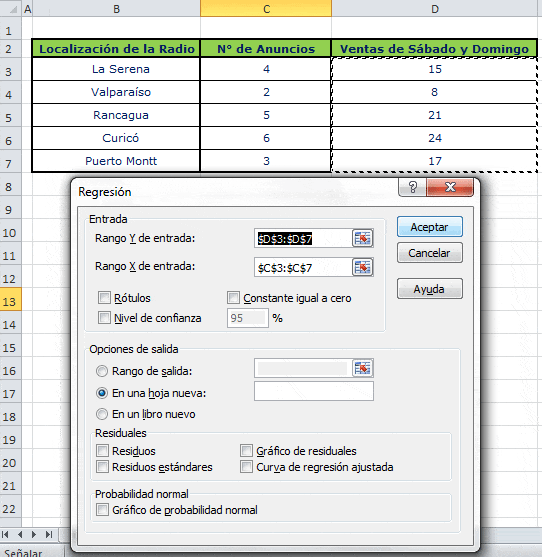
Ejemplo: Una empresa comercial tiene establecimientos en varias ciudades de Chile. El gerente comercial planea lanzar al aire un anuncio comercial por radio en las estaciones locales, al menos dos veces antes de una promoción (liquidación) que empezará el Sábado y terminará el Domingo. Planea tener las cifras de las ventas de grabadoras de vídeos (Blu-Ray) del Sábado y Domingo en sus diferentes locales y compararlas con el número de veces que apareció el comercial en la radio. El objetivo fundamental de la investigación es determinar si existe relación entre el número de veces que se transmitió el anuncio y las ventas de sus productos. Los datos son:

Con la información de la tabla anterior se desea responder las siguientes interrogantes:

1. ¿Cuál es la variable dependiente?. La variable dependiente son las Ventas.

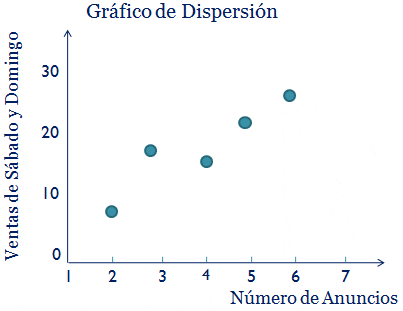
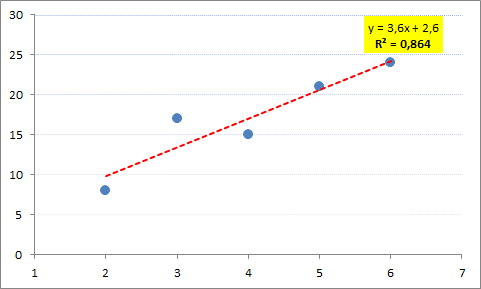
2. Trace el diagrama o gráfico de dispersión.

3. ¿Parece haber alguna relación entre X e Y?. Si existe una fuerte correlación positiva.
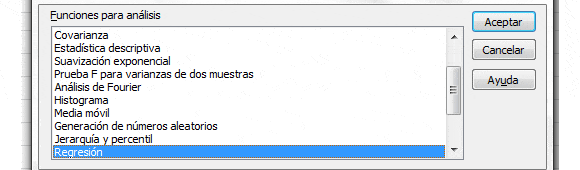
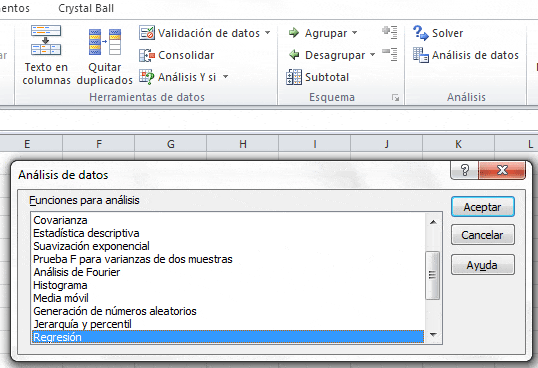
4. Determine el coeficiente de correlación. Para ello utilizaremos la herramienta de Análisis de Datos la cual se encuentra disponible en el menú de Datos de Excel. Luego seleccionamos Regresión según se observa a continuación:

En las opciones de regresión seleccionamos los datos de Ventas de Sábado y Domingo como Rango Y de entrada (variable dependiente) y los datos del N° de Anuncios corresponderá al Rango X de entrada (variable independiente).

Al seleccionar Aceptar se obtienen las estadísticas de la regresión donde el coeficiente de correlación de Pearson o r es de 0,93 (aproximado) y en consecuencia el coeficiente de determinación r² es de r²=(0,929516)²=0,864.

Notar que un procedimiento alternativo para obtener el coeficiente de determinación r² es mediante la incorporación de una línea de tendencia lineal en el diagrama de dispersión tal cual abordamos en el artículo Cómo utilizar una Regresión Lineal para realizar un Pronóstico de Demanda.

5. Evalúe la intensidad de la relación entre X e Y. 0,93 indica una correlación positiva fuerte entre el número de veces que sale publicado el anuncio, y las ventas.