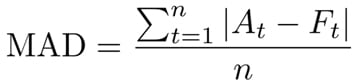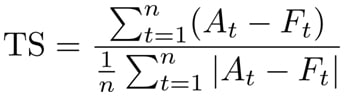Gestión de Operaciones

Cálculo del MAD y la Señal de Rastreo para un Pronóstico de Demanda

Un aspecto clave cuando se realiza un Pronóstico de Demanda es evaluar éste en cuanto a su ajuste respecto a la información real que se dispone. Para ello se introduce el concepto error que básicamente mide la diferencia entre el valor real y el valor pronosticado para un período específico.

Formalmente el error de un pronóstico $e_{t}$ se define como $e_{t}=A_{t}-F_{t}$ donde $A_{t}$ es la demanda real u observada en el período t y $F_{t}$ es la demanda pronosticada para el mismo período.

De esta forma, si por ejemplo, para un período dado (digamos por ejemplo, período 1), la demanda real es de 150 unidades y nuestro pronóstico para el mismo período fue 100 unidades, entonces $e_{1}=A_{1}-F_{1}=150-100=50>0$ , entonces tenemos una subestimación de la demanda real de una magnitud de 50 unidades.

De forma análoga, si la demanda real es de 150 unidades pero nuestro pronóstico para el mismo período, es, por ejemplo, 250 unidades el error correspondiente es $e_{1}=A_{1}-F_{1}=150-250=-100<0$ , por tanto en este caso tenemos una sobrestimación de la demanda real de una magnitud de 100 unidades.

En la práctica un pronóstico perfecto es imposible y por tanto el tomador de decisiones sabe que debe lidiar con un grado de error.

En este contexto se pueden identificar 2 tipos de errores: error sistemático el cual depende del método de pronóstico que utilizamos y el error aleatorio el cual es propio de la variación inherente de la situación que se modela. Luego, nos interesa minimizar la presencia y magnitud del error sistemático.

Para ello utilizamos 2 indicadores que generalmente se analizan en forma conjunta para tener una visión más objetiva de lo adecuado (o no) de un pronóstico de demanda. Dichos indicadores son el MAD y la Señal de Rastreo (TS). En este contexto a continuación se presentan las fórmulas para el cálculo del MAD y la Señal de Rastreo para un pronóstico de demanda haciendo uso de un método de series de tiempo.

MAD (Error Absoluto Medio): Que proporciona una medición del error promedio del pronóstico (en valor absoluto) y queda definido matemáticamente por:

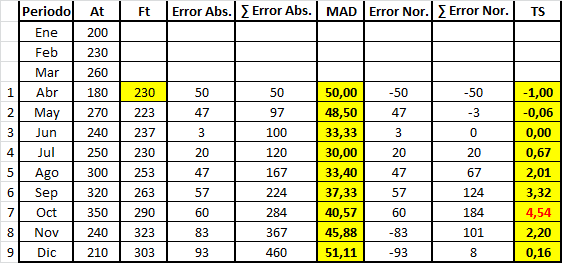
Señal de Rastreo (TS – Tracking Signal): Mide la desviación del pronóstico respecto a la variación de la demanda.

Cálculo del MAD y la Señal de Rastreo

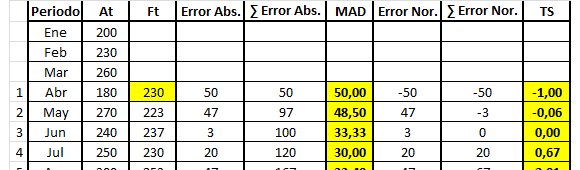
A continuación se presenta el cálculo del MAD y la Señal de Rastreo para el pronóstico de demanda de un producto determinado utilizando Media Móvil Simple con n=3. Notar que $A_{t}$ corresponde a la demanda real (observada) para el período (mes) t y $F_{t}$ es la demanda pronosticada para el mes t (obtenido a través del método de media móvil según lo señalado anteriormente).

El siguiente video tutorial muestra cómo se obtienen los resultados detallados en el resumen anterior:

En el artículo Interpretación de la Señal de Rastreo de un Pronóstico de Demanda detallamos la interpretación de este indicador que nos permite evaluar la presencia de error sistemático y si algún tipo de error (sobrestimación o subestimación) predomina en nuestras estimaciones.

Así también se propone revisar el aporte para efectos de evaluación que constituye disponer de un indicador de desempeño adicional denominado MAPE (Error Porcentual Absoluto Medio) que permite tener una estimación relativa (porcentual) del error del pronóstico.

¿Quieres tener el archivo Excel con el Cálculo del MAD y la Señal de Rastreo (TS) de este problema?.

[sociallocker]MUCHAS GRACIAS!. DESCARGA AQUÍ EL ARCHIVO[/sociallocker]

Problema de Transporte resuelto con Solver de Excel

Un Problema de Transporte consiste básicamente en determinar una política de distribución óptima que permita satisfacer los requerimientos de un determinado número de clientes asociado a la capacidad o logística de un cierto conjunto de oferentes.

Este tipo de problemas es una aplicación clásica de los modelos de Programación Lineal debido a que nos permite abordar problemas de naturaleza real y adicionalmente, se puede incorporar elementos adicionales que hacen más compleja la representación a través de un modelo de optimización, pero que, sin embargo, en la mayoría de los casos resulta ser más realista.

En el siguiente artículo podrás encontrar un vídeo que describe la formulación general de un problema de transporte básico, como también el detalle de un caso específico o instancia y su posterior resolución computacional.

Problema de Transporte

A continuación se presenta probablemente el caso más simple a considerar para un Problema de Transporte. Asumamos que tenemos 2 oferentes (P1 y P2) con capacidad de producción de 160.000 y 120.000 unidades de un producto homogéneo. Estos oferentes deben abastecer a 3 clientes (C1, C2 y C3) con demandas unitarias de 80.000, 70.000 y 90.000 unidades, respectivamente. El gráfico a continuación muestra sobre las flechas los costos unitarios de transporte entre un origen (oferente) a un cliente (demandante).

El problema consiste en determinar una política óptima de abastecimiento desde los oferentes a los demandantes de modo de cumplir los requerimientos y lograr los costos más bajos posibles. Para ello definiremos el siguiente modelo de Programación Lineal:

1. Variables de Decisión:

Xij : Unidades Transportadas desde la Planta i hasta el Cliente j (Con i=1,2, y j=1,2,3)

2. Función Objetivo:

Consiste en minimizar la función que representa los costos de transporte entre los oferentes y los demandantes.

Minimizar 3X11 + 4X12 + 6X13 + 5X21 + 3X22 + 5X23

3. Restricciones:

X11 + X21 = 80.000 (Satisfacer Demanda Cliente 1)
X12 + X22 = 70.000 (Satisfacer Demanda Cliente 2)
X13 + X23 = 90.000 (Satisfacer Demanda Cliente 3)
X11 + X12 + X13 <= 160.000 (Capacidad Planta 1)
X21 + X22 + X23 <= 120.000 (Capacidad Planta 2)
Xij >= 0 (No Negatividad)

Luego de implementar este modelo en Solver de Excel se obtiene la Solución Óptima: X11=80.000; X12=40.000; X13=0; X21=0; X22=30.000; X23=90.000. El Valor Óptimo (mínimo costo) es de $940.000. A continuación un video tutorial con el detalle de la resolución.

El ejemplo de transporte anterior es sin duda una de las versiones más sencillas que se puede encontrar de esta clase de problemas. Una extensión interesante y generalmente objeto de estudio en los cursos de Investigación de Operaciones es el Modelo de Transporte con Transbordo o Problema de Transbordo en una Red Logística de Transporte Multiperíodo.

Cómo resolver un modelo de Programación Lineal utilizando Solver de Excel

El complemento Solver de Excel nos permite resolver modelos de Programación Lineal de forma muy sencilla e intuitiva. Para ello necesitamos tener previamente Instalado el complemento de Solver en Excel. Sin embargo, en caso que el modelo a implementar sea de un mayor tamaño (usualmente más de 150 variables de decisión y 300 restricciones) a los que usualmente se abordan en cursos introductorios de Investigación Operativa se recomienda utilizar Premium Solver Pro tal como se describe en Cómo descargar e instalar la versión de Prueba de Premium Solver en Excel 2010.

En este contexto hemos desarrollado un tutorial que compara distintas herramientas computacionales para resolver modelos de optimización en una interfaz de Excel. Al respecto recomendamos al lector revisar el artículo: Solver, Premium Solver Pro y What’sBest! en la resolución del Problema de Localización y Transporte.

Cómo Resolver un modelo de Programación Lineal con Solver de Excel

El proceso se puede describir en 3 simples pasos y a continuación se aplica un problema típico de Producción y Transporte:

1. Definir las Variables de Decisión: Estas celdas serán las que estarán vinculadas a la función objetivo y restricciones a través de funciones lineales.

2. Definir la Función Objetivo: Esta celda debe ser única y ser adicionalmente una fórmula. Su valor dependerá del valor que se obtenga para las variables de decisión y su ponderación por los parámetros (constantes) que multiplican a dichas variables en la función objetivo.

3. Definir las Restricciones: Se recomienda dejar al Lado Derecho las constantes y al Lado Izquierdo fórmulas. El valor del Lado Izquierdo usualmente representa la ponderación de los parámetros relacionados con las restricciones con las variables de decisión.

El siguiente tutorial muestra la resolución de un modelo de Programación Lineal de dos variables utilizando Solver de Excel. Este ejemplo es similar al descrito en el Tutorial de Geogebra. Adicionalmente se pueden encontrar otros ejemplos resueltos en el Canal de Youtube de nuestro sitio cuya dirección es https://www.youtube.com/user/GEOTutoriales/videos.

Cómo resolver un modelo de Programación Lineal con Geogebra

En los cursos básicos de Investigación de Operaciones (o Investigación Operativa) frecuentemente el tema de introducción y discusión inicial es la formulación y resolución de modelos de optimización lineales para apoyar el proceso de toma de decisiones.

En este contexto se suelen abordar formulaciones matemáticas sencillas como los cubiertas en Programación Lineal y para entender sus propiedades se estudian modelos que consideran 2 variables de decisión para que sea factible y sencillo representarlos gráficamente, de modo de encontrar su solución óptima y valor óptimo (en caso de existir).

Al respecto cabe destacar que aquellas propiedades que se desprenden de la resolución gráfica de modelos lineales se pueden extender a problemas de Programación Lineal de mayor tamaño. Algunos de estos aspectos se detallan en el artículo Teorema Fundamental de la Programación Lineal.

A continuación presentaremos un modelo de Programación Lineal con 2 variables de decisión el cual resolveremos con la ayuda del software libre Geogebra, el cual es muy útil para la representación gráfica de funciones matemáticas, figuras geométricas, entre otras.

El programa se puede descargar gratuitamente tanto a computadores o smartphones, o si se prefiere, ejecutar directamente desde su página www.geogebra.org en Internet.

El siguiente tutorial de nuestro canal de Youtube muestra como resolvemos gráficamente este modelo de Programación Lineal utilizando el software Geogebra.

Una vista final de la representación gráfica del problema lineal propuesto se presenta a continuación:

Con color verde se destaca el polígono que considera todas aquellas soluciones factibles del problema, es decir, aquellos valores para las variables de decisión que satisfacen de forma simultanea el conjunto de restricciones. Dicho dominio de factibilidad se denomina región de puntos factibles o dominio de soluciones factibles.

Adicionalmente con color rojo se observa una linea punteada que representa la curva de nivel de la función objetivo que intercepta el vértice óptimo (solución óptima). La solución óptima es $X_{1}=100$ y $X_{2}=350$ , con valor óptimo $V(P)=3.100$ .

Cabe destacar que existen otras herramientas gráficas que permiten resolver gráficamente un modelo de Programación Lineal en 2 variables. Tal es el caso del software TORA el cual se incluye en el libro de Investigación de Operaciones de H.Taha (ver Cómo Resolver Gráficamente un Modelo de Programación Lineal con TORA) y IORTutorial (Cómo Resolver Gráficamente un Modelo de Programación Lineal con IORTutorial).

Bienvenido a Gestión de Operaciones

El Blog de Gestión de Operaciones nace en el mes de Julio del año 2011, teniendo por objetivo ser un referente para los estudiantes hispanos en el área de la Gestión de Operaciones, entregando información teórica y práctica para entender las principales temáticas de esta disciplina. En el Blog podrás encontrar tutoriales y ejemplos resueltos sobre optimización, gestión de inventarios, proyección de la demanda, plan de producción, proyectos, plan de requerimiento de materiales y otros temas de interés.

Si es primera vez que visitas nuestro Blog o si por el contrario ya eres un usuario recurrente, te sugerimos buscar información de interés para tus estudios siguiendo las recomendaciones que detallamos en la sección Cómo Comenzar. Al mes de Julio de 2016 y transcurridos más de 5 años de la puesta en marcha del sitio contamos con más de 250 publicaciones de calidad en diversos ámbitos de la Gestión de Operaciones y la Ingeniería Industrial.

¿Por qué un Blog? Principalmente para tener la oportunidad de mantener un contacto activo con nuestros usuarios y retroalimentarnos con sus consultas y aportes. Esto nos permite conocer de primera fuente cuáles son los temas de interés de nuestra audiencia y nos guía en la preparación de material académico a través de tutoriales.

Para mantenerte al tanto de las novedades del Blog puedes Suscribirte al Newsletter para lo cual encontrarás un Formulario de Suscripción en la barra lateral derecha del sitio y por supuesto te invitamos a visitarnos periódicamente.

Sin más que decir te damos la bienvenida a nuestro sitio y esperamos hacer una contribución significativa a tus estudios.